How to apply de Kelly criteria in your betting with the “Unit Impact” method
Note: This post is based on the following work. Barge-Gil, García-Hiernaux (Pyckio shareholders), A. (2019): Staking plans in sports betting under unknown true probabilities of the event. MPRA Working Paper 92196. University Library of Munich.
Kelly staking method has been shown to maximize long term growth of the bankroll (Kelly, 1956) and also median fortune (Ethier, 2004). The Kelly formula tells us that the percentage of bankroll to be staked in each bet is:
Stake = Expected Yield (EY) / (Odds – 1),
EY = Odds / True odds -1 where:
stake is the percentage of bankroll to be bet
true odds is the inverse of the true probability of the event
If the punter odds are 2.25 and the true odds are 2.20:
EY = 2.25/2.20-1 = 0.0227 = 2.27%
stake = 0.0227 / (2.25-1) = 0.0182 = 1.82%
That is, the Kelly formula advises to employ, for a given price, higher stakes the higher is the expected yield. On the other hand, for a given expected yield, stakes should be higher the lower is the price provided by the bookmaker
However, many professional tipsters do not use this staking method in practice. Why?
Because they say that they are able to estimate bets with positive expected value but they are not able to accurately estimate what is that EV; that is, they are not able to accurately estimate the true probability of events and therefore the true odds.
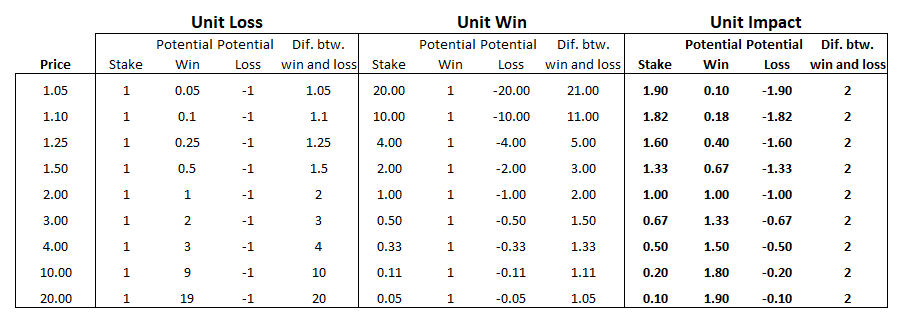
As a consequence, they usually rely on a flat stake (‘unit loss’) strategy (actually, around 60% of Pyckio PRO tipsters use this strategy). Note that this strategy shows the peculiarity that few bets (those placed at large prices) greatly determines the final bankroll. For example, a similar increase in bankroll is caused by a win at price 5 than by 8 straight wins at price 1.5.
An alternative, less frequently used, is to rely on a profit target or (“unit win”) strategy where the stake is a constant divided by (c – 1). This strategy holds constant the amount won in case of a win. This, obviously imply risking a very high stake in bets with lower prices. For example, to win a 1% of the bankroll at decimal price 1.1, 10% of the bankroll should be risked. However, if the decimal price is 2, only 1% of bankroll is to be risked.
To address this problem, Barge-Gil and García-Hiernaux (2019) propose an alternative staking method: the ‘UNIT IMPACT’. This method holds constant the difference in the bankroll between winning and losing instead of the amount lost in case of a loss or the amount won in case of a win. That is, every bet has exactly the same impact in the bankroll, no matter how long or short the price is. The formula for a unit impact staking method is simple, a flat amount divided by the decimal odds, instead of by the “decimal odds minus 1″ of the unit win method.
The following table provides an example on how the different staking plans work.
To compare the unit loss and the unit impact staking methods a crucial question is: How do they relate to the Kelly criterion?
The answer is that:
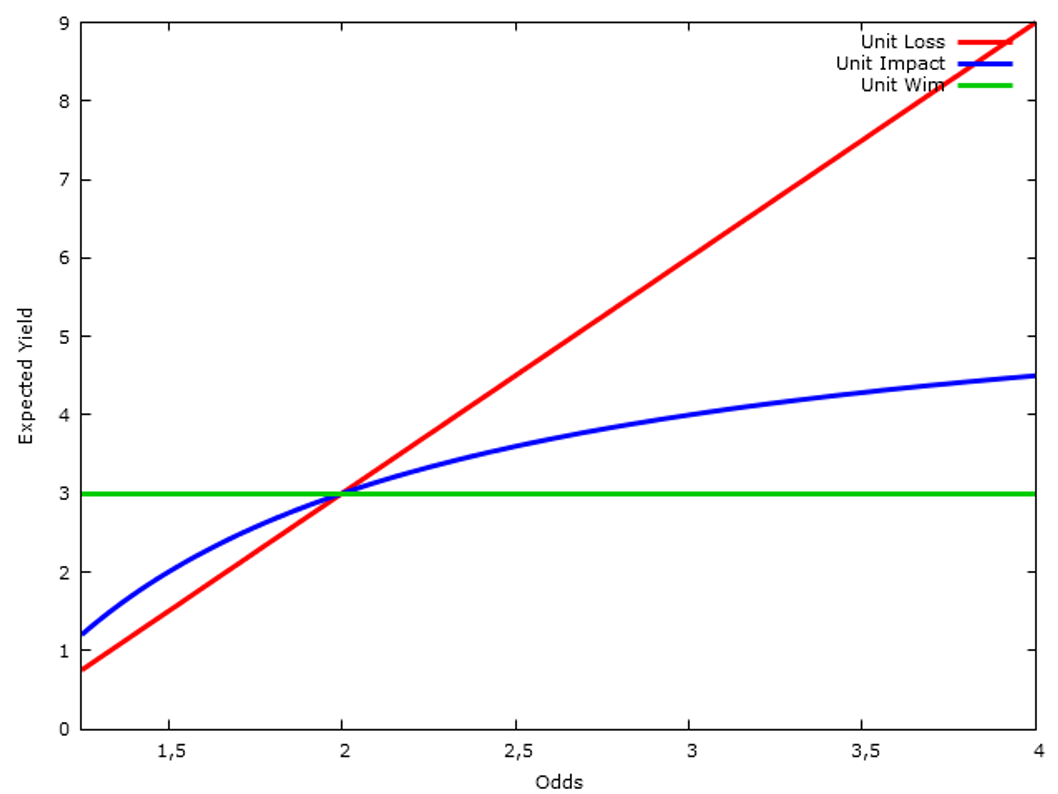
(i) if the expected yield of the tipster is unrelated to the odds then the Kelly staking method actually becomes the unit win method. Kelly makes you bet more, the higher the expected yield and vice versa. However, as the expected yield does not change, Kelly becomes a unit win method ((stake = 1 / odds-1)). That is, for punters whose track record does not point to a relationship between expected yield and the odds, using the profit target or unit win method would mean they are indeed betting as Kelly suggests.
(ii) if the expected yield of the tipster increases linearly with the odds, then the Kelly staking method actually becomes a flat stake or unit loss method, That is, if a tipster were able to correctly estimate the true probabilities for each event and the expected yield from these true probabilities increases linearly with the price, then the utilization of the Kelly criterion would actually result in a ’unit loss’ strategy. In other words, for tipsters or punters whose results prove to show a relationship between expected yield and the odds, a flat stake or unit loss method can be the best option if they want to bet like the Kelly method suggests.
(iii) ) if the expected yield of the tipster increases linearly with (c-1)/c (and, accordingly, non-linearly with c), then the Kelly method actually becomes the unit impact strategy. That is, for those whose track record show this relationship between EY and odds, the unit impact strategy is the one that is more close to the Kelly method. To increase linearly with (c-1)/c means that, the higher the odds, the higher the expected yield, but at a decreasing rate.
The following chart illustrates how the relationship between the expected yield and odds should be for each of the methods actually being the Kelly method.
Barge-Gil and García Hiernaux (2019) used the data from Pyckio to analyze which one of these relationships is actually taken place in practice by the Pyckio Tipsters.
They use two different methods: the analysis of bets by the PRO tipsters (to deal with survivorship bias, they only use bets placed since they reached the Grandmaster category) and the yield against closing odds.
The results of the analysis suggest that the relationship between expected yield and odds is in line with the one implied by the unit impact strategy and not by the one implied by either the unit win or unit loss strategies. That is, the relationship between the odds and the expected yield is more close to the blue line pattern. Of course there are exceptions, like the PRO Tipster nishikori, whose expected yield increases dramatically at the highest odds (what is quite uncommon if we consider the favorite long shot bias) and he might be best suited for the unit loss method. But overall, this study indicates that if you are a bettor and you use a variable bankroll you should consider the utilization of the simple rule of thumb provided by the unit impact strategy, as you would be approaching the Kelly criterion. Of course, if you were able to estimate the expected yield for every bet then you should use the Kelly criterion, but this is very unlikely. The unit impact strategy is, in a sense, a shortcut to the Kelly criterion. Moreover, from a psychological viewpoint, the unit impact strategy is a good method for any tipster or punter, as the impact of each bet in the bankroll, the difference between what you win and what you lose, is the same.
Unit Impact method: Stake = constant / Odds
In the table above you can see that the unit impact method makes you bet less, as long as the odds get higher, but no so less as the unit profit method suggests. You get a good reward if you win the higher odds, not so high as the profit obtained by the flat stakes method and of course not so low as the profits you would get under the unit won method On the other hand, it does not make you bet huge stakes at the lower prices, as the unit won method states. If you want to apply this method, just take as a reference the amount you use to bet at 2.0 odds. If it’s 100€ for example, the potential win is also 100€. Then the constant in the numerator is 200€, as 200/2.0 = 100. Use this constant and divide it for any odds to calculate the stake. For 1.50 odds you would bet 200/1.50 = 133.33€, for 3.0 you would bet 200/3.0 = 66.67€ and so on.
To complement this analysis they investigated the evolution of a variable bankroll under the different strategies and they found that the final bankroll using the unit impact staking method is much higher than the final bankroll under a unit loss strategy, while the unit win strategy is clearly the worse. In the original paper you can find the full analysis.
Andrés Barge-Gil
Alfredo García-Hiernaux
References:
Ethier, S. N. (2004). The kelly system maximizes median fortune. Journal of Applied Probability, 41(4):1230–1236.
Kelly, J. (1956). A new interpretation of information rate. Bell Sys. Tech. Journal, 35:917–926.




Hola Pyckio, un artículo muy interesante que describe de forma matemática y científica, las bondades de considerar una gestión de bankroll tal como la que proponen los autores. Mi más sincera enhorabuena por el trabajo realizado.
Ahora bien, según se propone en el artículo, para beneficiarnos de ésta modalidad de gestión de bankroll hay que considerar la cantidad (que no la unidad) que se apuesta a cuota 2.0.
Mi pregunta es la siguiente: ¿Qué criterio se utilizaría para definir la cantidad a apostar a cuota 2.0? En otras palabras, ¿cómo se calcula o bajo qué supuesto se calcularía la cantidad a apostar a cuota 2.0, la unidad, un % del bankroll, una cantidad fija o cómo se llevaría a cabo de forma correcta?
Por otra parte, ¿se consiguen rendimientos superiores ajustados al mismo riesgo objetivo bajo ésta modalidad de gestión del bankroll?
Enhorabuena a los autores y al equipo de Pyckio. Muy buen trabajo al respecto. Gracias de antemano y recibid un cordial saludo, hasta pronto.
Muchas gracias Antonio. Lo de la cuota 2.0 es porque hay que establecer una base, una referencia. Si tu tienes un bankroll de 3000€ y normalmente te juegas un 2% de tu bankroll a cuota 2.0 por ejemplo, esa es una referencia razonable. Esos 60€ serían la referencia para calcular el resto de stakes a diferentes cuotas. Con respecto a la otra pregunta, el método Kelly propone un método para que tus ganancias crezcan exponencialmente. Así que no podemos decir que incrementamos la rentabilidad con el mismo riesgo, “nada es gratis”.
I want it
3 comentario de “Cómo aplicar el criterio Kelly en tus apuestas con el método “Unit Impact””
3 comentario de “Cómo aplicar el criterio Kelly en tus apuestas con el método “Unit Impact””
Me gusta este método. Voy a aplicarlo a las apuestas en fútbol, en cuanto Real Madrid y Liverpool vuelvan a jugar.